I wanted to build an analog output for my Arduino, a DAC.
The default solution is to create a R-2R network like in the picture below.
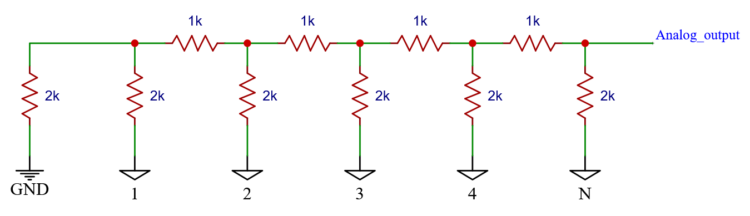
This resistor network needs 17 resistors to function. I do not have 2k resistors. The only values I have are up to 1 million ohm in these intervals 10, 12, 15, 18, 22, 27, 33, 39, 47, 56, 68, 82.
There is no double value of anything. The only way to make 2k resistors is two in series. So I would need 17+8 = 25 resistors in total.
So then I asked myself; can it be done with only eight resistors? Like in the picture below. The answer turned out to be: Yes, almost, and I had to make a Python script to generate the needed resistor values and combinations.
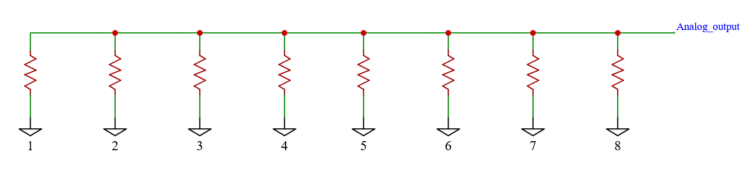
Table of Contents
- My resistor collection
- Random selection approach
- Select each 8 bit value
- Solving the resistor network
- Scoring and sorting the results
- Some tweaking
- Building the DAC
- Arduino sketch
- Time for the oscilloscope
- Video
- DAC Generator
My resistor collection
First thing to do is tell the script which resistors I own.
my_resistors = [10, 12, 15, 18, 22, 27, 33, 39, 47, 56, 68, 82,
100, 120, 150, 180, 220, 270, 330, 390, 470, 560, 680, 820,
1000, 1200, 1500, 1800, 2200, 2700, 3300, 3900, 4700, 5600, 6800, 8200,
10000, 12000, 15000, 18000, 22000, 27000, 33000, 39000, 47000, 56000, 68000, 82000,
100000, 120000, 150000, 180000, 220000, 270000, 330000, 390000, 470000, 560000, 680000, 820000,
1000000, 1200000, 1500000, 1800000, 2200000, 2700000, 3300000, 3900000, 4700000, 5600000, 6800000, 8200000,
10000000]
This is just array with all the common Ebay-kit values.
Random selection approach
For a 8 bit DAC, the amount of resistor combinations to check is millions. Therefore I am going to take a random selection of resistor combinations and see what results I can get from that.
def simulate(resistors):
pass
def main():
my_results = []
for i in range(0, 1000):
resistors = random.sample(my_resistors, 8)
result = simulate(resistors)
my_results.append(result)
if __name__ == '__main__':
main()
This is the basic framework that will run the simulations. I now select 8 random resistors and pass them to the simulate function.
Select each 8 bit value
For each possible 8 bit value, the resistors will each be connected to either 5V or 0V depending on the state of the bit they are connected to. The network therefore will output a different analog voltage for each combination.
def solve_network(resistors, binary):
pass
def simulate(resistors):
voltages = []
for i in range(0, 256):
binary = f'{i:08b}'
v = solve_network(resistors, binary)
voltages.append(v)
return resistors, voltages
Solving the resistor network
I then need the script to solve the resister network and tell me the voltage for this specific binary number and the selected resistors.
def solve_network(resistors, binary):
voltage = 0
step = 5
while step > 0.01:
current = 0
for i in range(len(resistors)):
if binary[i] == '1':
current += (5 - voltage) / resistors[i]
else:
current -= voltage / resistors[i]
if current > 0:
voltage += step
if current < 0:
voltage -= step
if current == 0:
break
step /= 2
return binary, voltage
def simulate(resistors):
binary_voltages = []
for i in range(0, 256):
binary = f'{i:08b}'
bv = solve_network(resistors, binary)
binary_voltages.append(bv)
return resistors, binary_voltages
The script now produces some results. See the picture below.
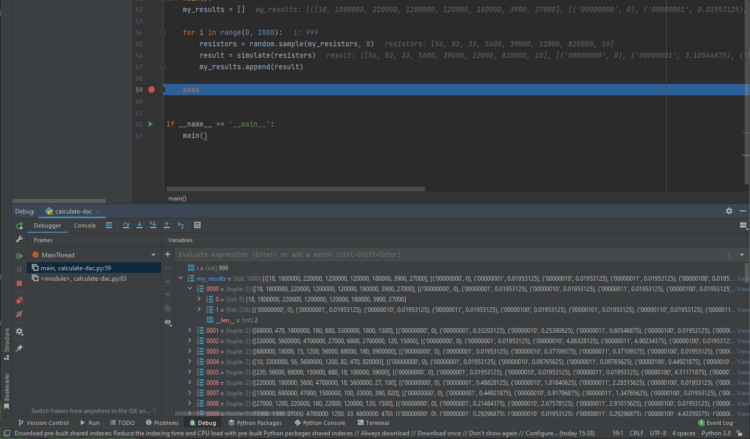
I put a debug break on the last command in the script so we can inspect. The my_results now has 1000 tested resistor combinations. The results are in the form of a tupple containing the resistors, and the resulting voltage of the binary combination applied to them.
Scoring and sorting the results
In order to sort, I need some way to put a value on each result.
def evaluate(binary_voltages):
total_score = 0
organized_binary_voltages = []
for i in range(0, 256):
target = 5 / 255 * i
score = math.inf
best_b = None
best_v = None
for b, v in binary_voltages:
if abs(target-v) < score:
score = abs(target-v)
best_b = b
best_v = v
organized_binary_voltages.append([best_b, best_v])
total_score -= score / 256
return total_score, organized_binary_voltages
This function creates a range of 256 voltages from 0V to 5V, it then tries to find a voltage in the list created earlier that best matches the target voltage.
The difference between actual an targeted voltage is subtracted from the total score, and the binary voltage combination is stored in organized_binary_voltages.
With that list we can just look up a number from 0 to 255 and get a binary combination that gives us the request voltage.
Some tweaking
After some tweaking, the main routine now returns forever and spits out the best resistor combinations and associated results.
def main():
my_results = []
best_score = -math.inf
i = 0
while True:
i += 1
print('\r', i, end='')
resistors = random.sample(my_resistors, 8)
result = simulate(resistors)
my_results.append(result)
score = result[0]
if score > best_score:
best_score = score
print(result)
print(i, end='\r')
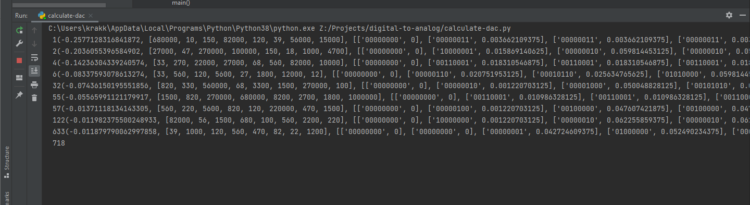
This produces the following output, every time a better solution is found, it is written to the console.
After running the program for half an hour I took the last line and with some editing pasted this into Excel. There I also calculated the target data and made a line-graph of both these lists.
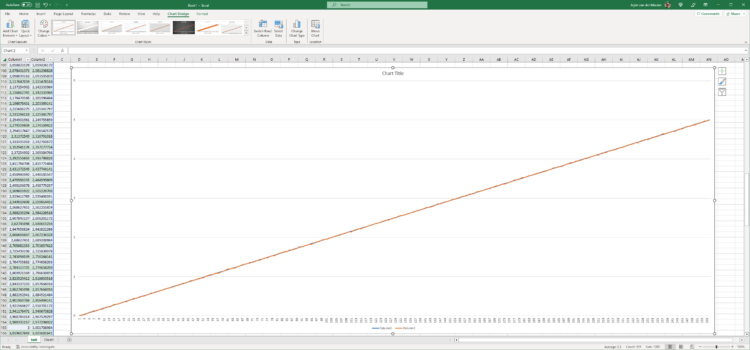
If we zoom in on the image we can see some small deviations, these are also calculated by the script and are in fact part of the scoring factor.
Building the DAC
The program gives me a list in the form [560, 180, 1200, 33, 120, 15, 150, 56], I then need to upscale these resistors to have the network not draw too much current. Just add two zeros and all will be OK.
In the order of that list the resistors have to be connected to pins PD7 to PD0. Which form a single port on de nano, port D. The other end of the resistors have to be connected into a single output. For this I chose a voltage rail on the breadboard.
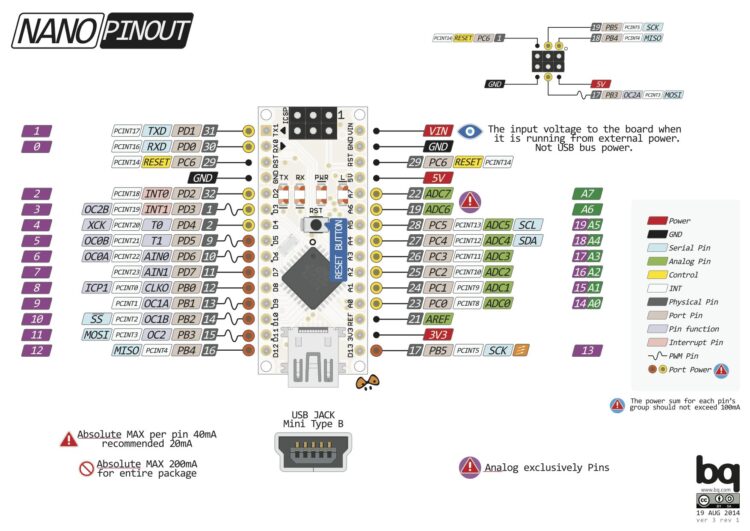

Please note that PD0 and PD1 are in reverse order compared to the other ones.
Arduino sketch
I converted the organize_binary_voltages into a c++ array and made a sketch that output a sine wave.
// Resistors PD7-0 > 82K, 56K, 47K, 22K, 15K, 8.2K, 3.9K, 1.8K
int bits[] = {0b00000000, 0b10000000, 0b01000000, 0b00100000, 0b11000000, 0b10100000, 0b01100000, 0b00010000, 0b11100000,
0b10010000, 0b01010000, 0b00001000, 0b00110000, 0b11010000, 0b10001000, 0b10110000, 0b01001000, 0b01110000,
0b00101000, 0b11001000, 0b11110000, 0b10101000, 0b01101000, 0b00011000, 0b11101000, 0b00000100, 0b10011000,
0b01011000, 0b00111000, 0b10000100, 0b01000100, 0b11011000, 0b00100100, 0b10111000, 0b01111000, 0b11000100,
0b10100100, 0b01100100, 0b11111000, 0b00010100, 0b11100100, 0b10010100, 0b01010100, 0b00001100, 0b00110100,
0b11010100, 0b10001100, 0b10110100, 0b01001100, 0b01110100, 0b00101100, 0b11001100, 0b11110100, 0b10101100,
0b01101100, 0b00011100, 0b11101100, 0b10011100, 0b01011100, 0b00111100, 0b00000010, 0b11011100, 0b10111100,
0b10000010, 0b01111100, 0b01000010, 0b00100010, 0b11111100, 0b11000010, 0b10100010, 0b01100010, 0b00010010,
0b11100010, 0b10010010, 0b01010010, 0b00001010, 0b00110010, 0b11010010, 0b10001010, 0b10110010, 0b01001010,
0b01110010, 0b00101010, 0b11001010, 0b11110010, 0b10101010, 0b01101010, 0b00011010, 0b11101010, 0b00000110,
0b10011010, 0b01011010, 0b00111010, 0b10000110, 0b01000110, 0b11011010, 0b00100110, 0b10111010, 0b01111010,
0b11000110, 0b10100110, 0b01100110, 0b11111010, 0b00010110, 0b11100110, 0b10010110, 0b01010110, 0b00001110,
0b00110110, 0b11010110, 0b10001110, 0b10110110, 0b01001110, 0b01110110, 0b00101110, 0b11001110, 0b11110110,
0b10101110, 0b01101110, 0b00011110, 0b11101110, 0b10011110, 0b01011110, 0b00111110, 0b11011110, 0b10111110,
0b01111110, 0b11111110, 0b00000001, 0b10000001, 0b01000001, 0b00100001, 0b11000001, 0b10100001, 0b01100001,
0b00010001, 0b11100001, 0b10010001, 0b01010001, 0b00001001, 0b00110001, 0b11010001, 0b10001001, 0b10110001,
0b01001001, 0b01110001, 0b00101001, 0b11001001, 0b11110001, 0b10101001, 0b01101001, 0b00011001, 0b11101001,
0b00000101, 0b10011001, 0b01011001, 0b00111001, 0b10000101, 0b01000101, 0b11011001, 0b00100101, 0b10111001,
0b01111001, 0b11000101, 0b10100101, 0b01100101, 0b11111001, 0b00010101, 0b11100101, 0b10010101, 0b01010101,
0b00001101, 0b00110101, 0b11010101, 0b10001101, 0b10110101, 0b01001101, 0b01110101, 0b00101101, 0b11001101,
0b11110101, 0b10101101, 0b01101101, 0b00011101, 0b11101101, 0b10011101, 0b01011101, 0b00111101, 0b00000011,
0b11011101, 0b10111101, 0b10000011, 0b01111101, 0b01000011, 0b00100011, 0b11111101, 0b11000011, 0b10100011,
0b01100011, 0b00010011, 0b11100011, 0b10010011, 0b01010011, 0b00001011, 0b00110011, 0b11010011, 0b10001011,
0b10110011, 0b01001011, 0b01110011, 0b00101011, 0b11001011, 0b11110011, 0b10101011, 0b01101011, 0b00011011,
0b11101011, 0b00000111, 0b10011011, 0b01011011, 0b00111011, 0b10000111, 0b01000111, 0b11011011, 0b00100111,
0b10111011, 0b01111011, 0b11000111, 0b10100111, 0b01100111, 0b11111011, 0b00010111, 0b11100111, 0b10010111,
0b01010111, 0b00001111, 0b00110111, 0b11010111, 0b10001111, 0b10110111, 0b01001111, 0b01110111, 0b00101111,
0b11001111, 0b11110111, 0b10101111, 0b01101111, 0b00011111, 0b11101111, 0b10011111, 0b01011111, 0b00111111,
0b11011111, 0b10111111, 0b01111111, 0b11111111};
// https://www.daycounter.com/Calculators/Sine-Generator-Calculator2.phtml
int sine[] = {128,129,131,132,134,135,137,138,140,142,143,145,146,148,149,151,152,154,155,157,158,160,162,163,165,166,167,
169,170,172,173,175,176,178,179,181,182,183,185,186,188,189,190,192,193,194,196,197,198,200,201,202,203,205,
206,207,208,210,211,212,213,214,215,217,218,219,220,221,222,223,224,225,226,227,228,229,230,231,232,233,234,
234,235,236,237,238,238,239,240,241,241,242,243,243,244,245,245,246,246,247,248,248,249,249,250,250,250,251,
251,252,252,252,253,253,253,253,254,254,254,254,254,255,255,255,255,255,255,255,255,255,255,255,255,255,255,
255,254,254,254,254,254,253,253,253,253,252,252,252,251,251,250,250,250,249,249,248,248,247,246,246,245,245,
244,243,243,242,241,241,240,239,238,238,237,236,235,234,234,233,232,231,230,229,228,227,226,225,224,223,222,
221,220,219,218,217,215,214,213,212,211,210,208,207,206,205,203,202,201,200,198,197,196,194,193,192,190,189,
188,186,185,183,182,181,179,178,176,175,173,172,170,169,167,166,165,163,162,160,158,157,155,154,152,151,149,
148,146,145,143,142,140,138,137,135,134,132,131,129,128,126,124,123,121,120,118,117,115,113,112,110,109,107,
106,104,103,101,100,98,97,95,93,92,90,89,88,86,85,83,82,80,79,77,76,74,73,72,70,69,67,66,65,63,62,61,59,58,
57,55,54,53,52,50,49,48,47,45,44,43,42,41,40,38,37,36,35,34,33,32,31,30,29,28,27,26,25,24,23,22,21,21,20,19,
18,17,17,16,15,14,14,13,12,12,11,10,10,9,9,8,7,7,6,6,5,5,5,4,4,3,3,3,2,2,2,2,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,1,1,1,1,1,2,2,2,2,3,3,3,4,4,5,5,5,6,6,7,7,8,9,9,10,10,11,12,12,13,14,14,15,16,17,17,18,19,20,21,21,
22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,40,41,42,43,44,45,47,48,49,50,52,53,54,55,57,58,59,61,62,
63,65,66,67,69,70,72,73,74,76,77,79,80,82,83,85,86,88,89,90,92,93,95,97,98,100,101,103,104,106,107,109,110,
112,113,115,117,118,120,121,123,124,126};
void setup() {
// put your setup code here, to run once:
DDRD = B11111111; // set PORTD (digital 7~0) to outputs
}
void loop() {
for (int i=0; i<512; i++) {
int j = sine[i];
PORTD = bits[j];
}
}
Time for the oscilloscope
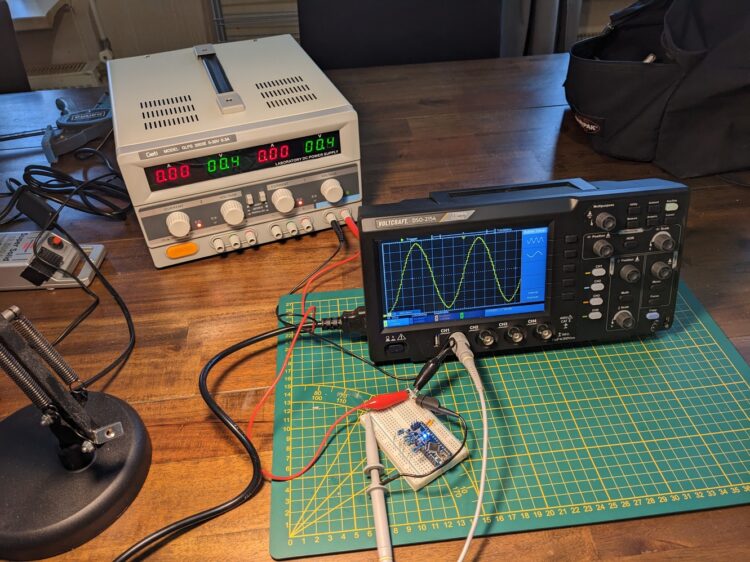
The sine-wave looks a bit bumpy. In the sketch above you can see the sine-wave-lookup table only has 50 points. This DAC has resolution for 500 points, but that is something I will test another day.
Video
DAC Generator
I made an online tool to do all the calculating and coding for you. Give it a try!
One thought on “Creating the 8 bit 8 resistor DAC”